Η ένταση ρεύματος, που διαρρέει ένα αγωγό κυκλώματος, είναι ανάλογη της τάσεως που εφαρμόζεται στα άκρα του αγωγού και αντίστροφα ανάλογη της αντιστάσεώς του.
[παράδειγμα]
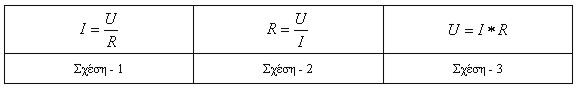
από τη σχέση 1 προκύπτουν και οι σχέσεις 2 & 3.
Το αριθμητικό άθροισμα των ρευμάτων που φθάνουν σε ένα κόμβο, είναι ίσο με το άθροισμα των ρευμάτων που φεύγουν από αυτόν.
[παράδειγμα]
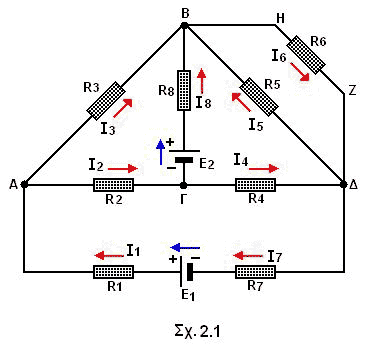
Στο σχήμα 2.1 έχουμε π.χ. με τις φορές των ρευμάτων όπως είναι σχεδιασμένες:
Για τον κόμβο Α : Ι1 = Ι 2 + Ι3 (1)
Για τον κόμβο Β : Ι3 + Ι8 + Ι5 = Ι6 (2)
Για τον κόμβο Δ : Ι4 + Ι6 = Ι5 + Ι7 (3)
Οι σχέσεις (1) έως (3) γράφονται επίσης :
Ι1 - Ι2 - Ι3 = 0 (4) ή Ι2 + Ι3 - Ι1 = 0 (5)
Ι3 + Ι8 + Ι5 - Ι6 = 0 (6) ή Ι6 - Ι3 -Ι8 -Ι5 = 0 (7)
Ι4 + Ι6 - Ι5 - Ι7 = 0 (8) ή Ι5 + Ι7 - Ι4 - Ι6 = 0 (9)
και γενικά : Σ Ι=0 (10)
Από τις σχέσεις (4) έως (9) και τη γενική σχέση (10) εξάγεται το συμπέρασμα, ότι, αν θεωρήσουμε τα ρεύματα που φθάνουν σε ένα κόμβο θετικά και αυτά που φεύγουν αρνητικά όπως στις εξισώσεις (4), (6) και (8) ή αντίστροφα τα ρεύματα που φθάνουν αρνητικά και αυτά που φεύγουν θετικά [όπως στις εξισώσεις (5), (7) και (9)], μπορούμε να διατυπώσουμε ως εξής τον πρώτο κανόνα του Kirchhoff :
Το αλγεβρικό άθροισμα των ρευμάτων που συναντώνται σε ένα κόμβο είναι ίσο με το μηδέν.
Το αλγεβρικό άθροισμα των ηλεκτρεγερτικών δυνάμενων ενός βρόχου είναι ίσο με το αλγεβρικό άθροισμα των πτώσεων τάσεως τους κλάδους του βρόχου.
[παράδειγμα]
Σ E = Σ IR (11)
Στο βρόχο του σχήματος 3.1 έχουμε : E1 - E2 = -I2R2 - I3R3 + I4R4 - I5R5 + I6R6 - I7R7 (12)
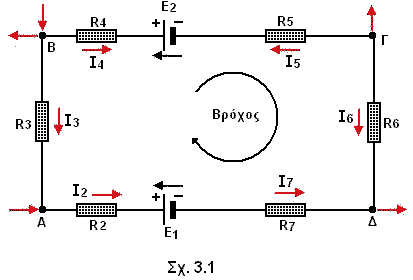
Για κάθε βρόχο ενός κυκλώματος, μπορούμε να γράψουμε μια εξίσωση της μορφής (11). Αν ένας βρόχος δεν περιλαμβάνει ηλεκτρεγερτικές δυνάμεις, τότε το άθροισμα των πτώσεων τάσεως στις καταναλώσεις του βρόχου είναι ίσο με το μηδέν :
Σ IR = Σ U=0 (13)
Αντί της ΗΕΔ Ε, χρησιμοποιούμε σε ορισμένες περιπτώσεις την πολική τάση U μιας πηγής, την οποία σημειώνουμε με φορά από το θετικό πόλο προς τον αρνητικό (αντίθετα δηλαδή από τη φορά της Ε) και τη μεταχειριζόμαστε σαν μια πτώση τάσεως στην εφαρμογή του δεύτερου κανόνα του Kirchhoff.
Με το δεύτερο κανόνα του Kirchhoff αποδεικνύεται αμέσως ότι:
Η διαφορά των δυναμικών δύο σημείων είναι ίση με την τάση μεταξύ των δύο σημείων.
ΠΑΡΑΔΕΙΓΜΑΤΑ
Παράδειγμα 1.
Από ένα αντιστάτη R = 2000 Ω, περνά ρεύμα εντάσεως I = 50 mA. Να βρεθεί η τάση, που εφαρμόζεται στα άκρα του αντιστάτη.
Λύση
Ι = 50mA = 50 x 10 -3 A = 0,05 A
Από τη σχέση (3) : U=I x R = 0,05 x 2000 = 100 V
Άρα η τάση που εφαρμόζεται στα άκρα του αντιστάτη R είναι : U = 100 V

|

